HiFloat8:高性能训练之路
2025-12-19
以下文章来源于微信公众号——全球计算联盟GCC
本期文章将介绍HiFloat8高性能训练算法及比较优势,如需回顾HiFloat8数据格式,请参看上期文章《HiFloat8浮点数据格式:既要又要之路》
Float8单数据格式FP8/HiF8训练 算法介绍
1.1 Float8混合精度训练策略
随着预训练模型(尤其是基于Transformer架构的大语言模型)参数规模突破千亿级,训练过程面临愈发严重的算力和内存瓶颈,成本极高。在此背景下,8位浮点逐渐成为学术界与工业界的关键突破方向,特别是在支持矩阵乘加速器的GPU和NPU上,相对16位浮点呈现出显著性能优势。当前推向商用的Float8单数据格式主要包括FP8(E4M3/E5M2)和HiF8。本节简要介绍Float8混合精度预训练的基本原理,方便读者进一步理解后续内容。
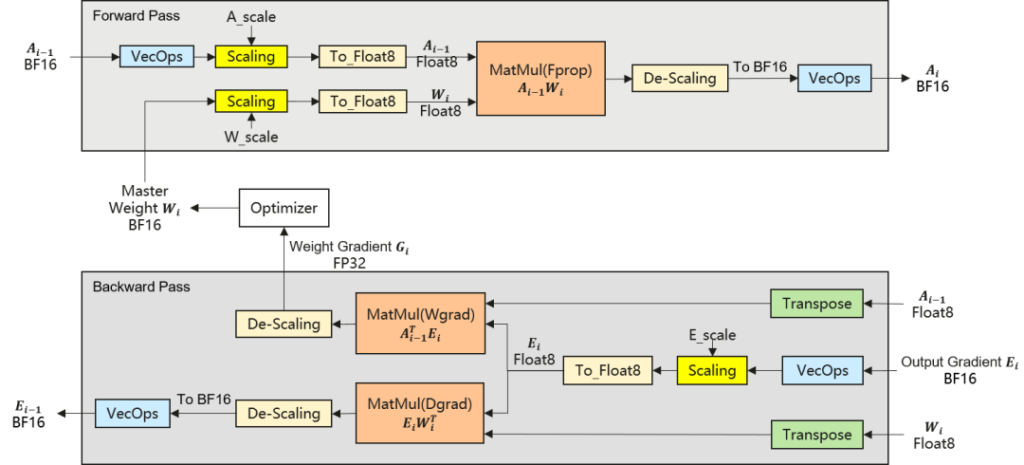
图一. Float8混合精度训练流程示意图
在实际训练中Float8通常采用混合精度策略,即对计算密集且对精度敏感度较低的模块(如稠密线性层、MoE 专家层、Attention中QKV投影)使用Float8计算;而对归一化算子、MoE门控、优化器等高敏感模块仍保持FP32/BF16精度。图 1 展示了Float8混合精度训练流程。如图所示在每个transformer block的前向与反向计算过程中,矩阵乘相关计算(Fprop/Wgrad/Dgrad)以Float8执行,以实现显著的加速与显存节省。图1中的VecOps模块指不含矩阵乘法的Vector操作,例如Softmax、Residual Add、SwiGLU激活函数等等。To_Float8模块是指将数据从高精度BF16量化到Float8格式。可以看到,激活值A,权重W,和激活值梯度E,在进入矩阵乘单元之前,都先进行了Per-Tensor Scaling的操作(也可以是更细粒度Scaling),然后才Cast到Float8执行乘法;同时,矩阵计算完成后,输出结果还需要进行De-Scaling还原。这是因为现在的语言模型的数据范围极其分散,Float8通常无法直接覆盖需求的动态范围,因此需要通过缩放来把数据有效值移动到格式有限的表达范围内。而Float8的Scaling策略和粒度,是混合精度训练稳定性和收敛性所面临的关键挑战,下面将对这部分内容展开讨论。
1.2 Float8 Current Scaling & Delayed Scaling训练策略介绍
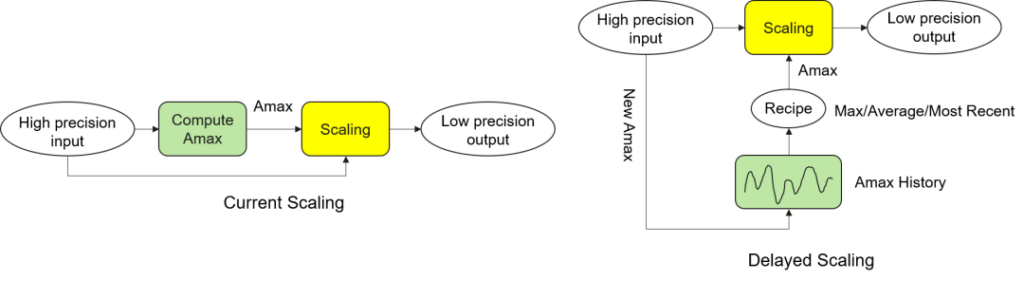
图二. Current Scaling VS Delayed Scaling
高精度数据转换到低精度一般需要做缩放处理Scaling,或者称之为量化。假设给定一种量化粒度获得一个数据块记为X,Scaling的过程是给X乘上一个系数,使得所有值比较安全地转化到低比特的表达范围内,这个系数我们称之为缩放因子(或者称为Scaling Factor)。现有的量化方法分为Current Scaling(或者叫In-time Scaling)和Delayed Scaling。式(1)和式(2)描述了Current Scaling执行缩放的原理。其中F8max是指该8比特浮点可表示的最大值(例如FP8-E4M3为448)。Amax是指X中所有数值统计的最大绝对值。式(1)计算得到的Scale变量等价于缩放因子。式(2)表示高精度数据缩放到低精度表达范围内的缩放过程。
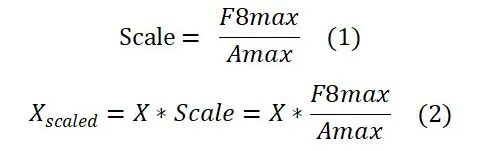
如图二所示,Current Scaling是指在当前高精度数据X的基础上遍历所有数值获得Amax,可以通过执行ComputeAmax(如torch.max())计算。但这种方式的问题是当X的规模比较大的时候,Amax的计算会引入显著的延迟开销。而矩阵乘法只能等待式(1)中的Scale计算完成后才能开始,最终会影响端到端性能。如果我们能提前预测当前X的Amax的近似值,Amax的精确求解和矩阵乘的计算就可以实现解耦并行执行,从而很大程度减少Amax计算对训练性能的影响。这种基于近似的Amax来做缩放的策略则是Delayed Scaling。
Delayed Scaling的理论原理如式(3)和式(4)所示。与Current Scaling不同的是右边多乘了一项安全参数
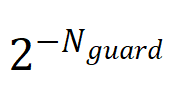
,其中Nguard代表防止上溢的安全阈值参数,例如FP8一般设为3,HiF8一般设为8~12。
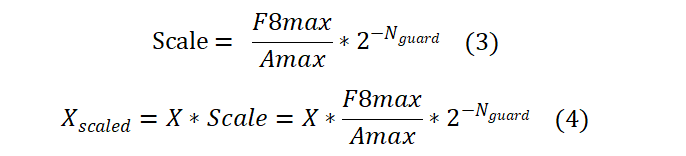
Delayed Scaling的核心思想是通过当前数据X在历史迭代步中的统计信息来对当前的Amax进行近似估计。具体做法是通过建立一个Amax History Buffer来缓存X在若干历史迭代步中的最大值统计结果。当需要Amax时,会从History Buffer中选出一个最大值(也可以是其他规则,如最邻近的,和均值)来作为当前Amax的估计,并据此完成式(3)与式(4)所定义的缩放操作。与此同时,我们可基于给定的统计间隔参数Interval来计算真实的Amax,并追加到History Buffer中。例如,当Interval=1时, 表示每次迭代都会计算一次当前X的Amax;而当Interval=5时, 则表示每5次迭代才计算一次当前X的Amax(中间4次不进行统计)。由于History Buffer具有固定容量,所以当新的Amax追加到History Buffer末尾后,最前面的队首信息会被丢弃掉。这样,可以一直用最近的历史信息来估计当前的Amax。理论上,在Amax的近似误差不显著影响训练数值稳定性时,Delayed Scaling相较于Current Scaling具有更优的训练性能潜力,并且Amax统计频率越低,其带来的训练性能加速收益理论上越显著。
Float8块浮点格式MXFP8训练算法介绍
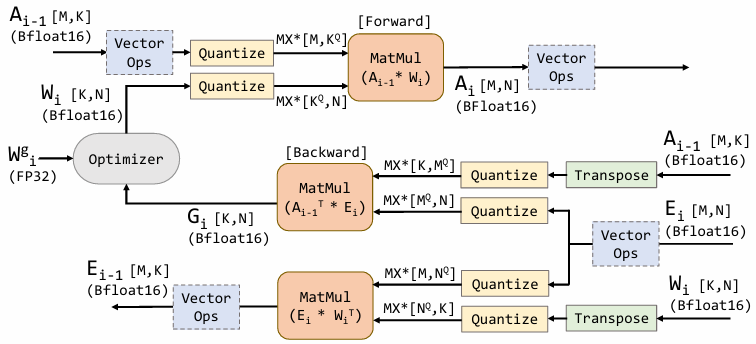
最新面向NVIDIA Blackwell平台的MXFP8(Micro-scaling FP8)则进一步采用1×32更细粒度的量化,并使用硬化的UE8M0格式记录Scaling因子。用户可对张量按行或者按列划分成连续块Block,每个块包含32个连续值,这与Blackwell Tensor Cores的设计相匹配。其中每个块分配了一个以E8M0格式存储的专用缩放因子。图三展示了使用MXFP8的预训练流程。其中在前向过程中,激活值A和权重W分别需要按行和按列进行量化,才能进行后续的乘法。因为Tensor Core只能支持左矩阵按行量化,右矩阵按列量化的块浮点输入,进而才能正确完成矩阵乘法运算。在反向过程中,输出值的梯度E则需按行和按列分别做两次量化(权重梯度和激活值梯度矩阵乘运算中,E一个是右矩阵,一个左矩阵),比单数据浮点格式多出了一次量化。同时在反向过程中,还需要对激活值A和权重W的高精度备份先做转置,然后分别按列和按行再次进行量化(单数据浮点格式不需要)。原因是前向的量化发生在特定方向,MXFP8张量直接转置后,反向数据不满足Tensor Core矩阵乘的输入要求。相比8-bit单数据格式训练只需要对A、W和E三个Tensor各做一次量化,MXFP8在训练流程的关键路径上都需要对三个Tensor按行和按列两个方向分别进行量化,这多出的量化操作大幅影响了加速性能。即便MXFP8硬化了E8M0的Scale,矩阵乘不会在K轴频繁断流,对训练性能有所提升,但也很难弥补由上述训练流程结构性复杂化所引入的性能劣化。从训练流程机理的角度来看,块浮点格式由于其方向敏感的缩放与额外的量化依赖,其端到端训练性能在理论上天然弱于采用粗粒度Scaling策略的单数据浮点格式。
Float8训练性能对比分析
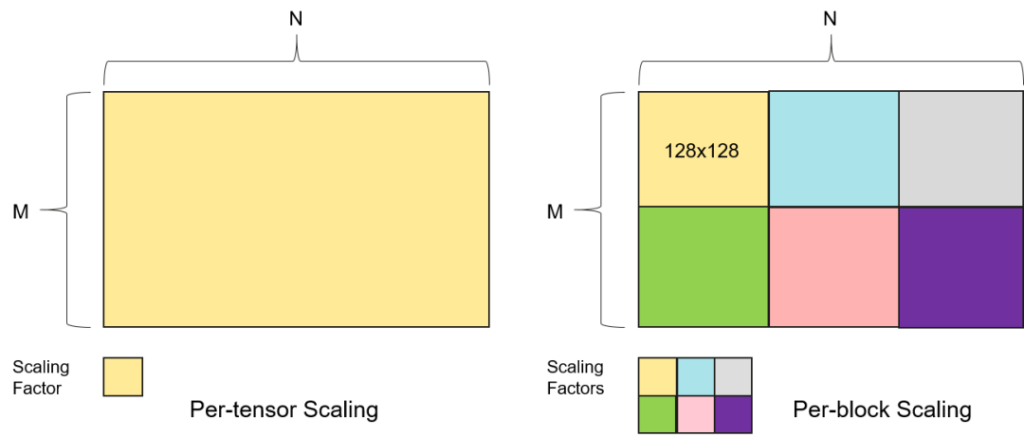
图四. Per-tensor和Per-block Scaling
在预训练中常用的量化粒度包括Per-tensor Scaling和Per-block Scaling。如图四所示,Per-tensor Scaling是指为每个Tensor分配唯一的缩放系数,用于量化Tensor内全部数值。然而,大型模型的Tensor内部往往包含显著不同的数值分布,例如不同注意力头的权重规模不同,SwiGLU或MoE Router的激活函数会产生异常稀疏或极值集中的病态矩阵。Per-block Scaling将每个Tensor划分为更小、更易于管理的连续块,并为每个Tensor Block分配专用的缩放因子。缩放机制可以适配局部数值分布而非受极端值主导。这意味着高数量级区域得到准确表示,而不会影响同一Tensor内更小值的保真度。现有流行的FP8 Training Recipe之一会将Input和Gradient以1×128的1D Tile进行量化、Weight以128×128的2D Tile进行量化,例如DeepSeek-V3或者Transformer Engine。
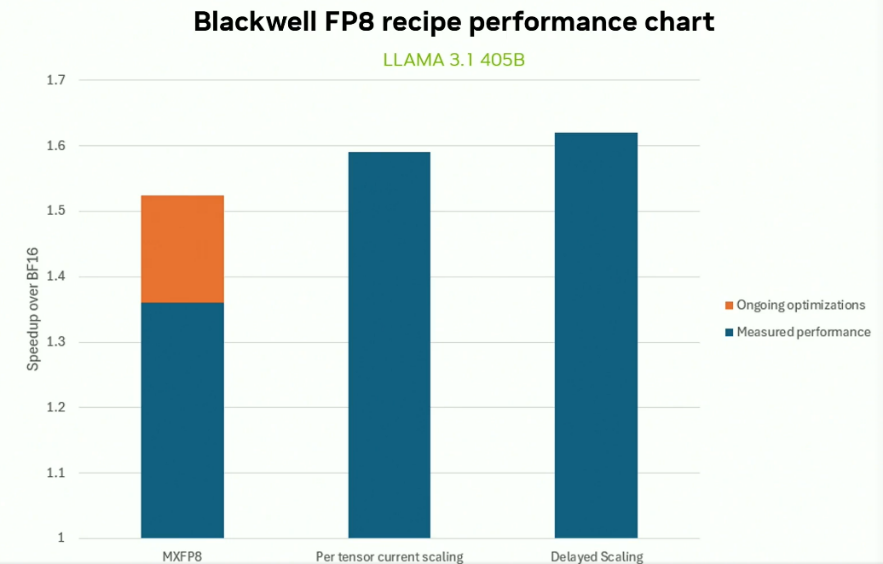
图五. Delayed Scaling相比Current Scaling的加速效果[2]
MXFP8为了减少整体溢出风险,将原数据切成包含32个值的连续块的粒度来量化。这在保持高稳定性训练的同时引入了额外的反向量化开销,理论上端到端训练性能不如粗粒度缩放的单数据浮点格式。如图五公开资料所示,在LLAMA 3.1 405B模型的预训练中,MXFP8相比纯BF16训练带来了约1.36x的加速比(预期进一步软件优化的上限是1.52x),低于Per-tensor FP8 Current Scaling的1.58x以及Per-tensor FP8 Delayed Scaling(Interval=1)的1.62x加速比。同时,该结果也佐证了Current Scaling的训练性能低于Delayed Scaling。图五结果进一步表明,当Amax统计频次Interval=1的时候,Per-tensor Delayed Scaling比Per-tensor Current Scaling具有约4%的额外性能增益。这里Interval=1是指第0个迭代步计算一次真实的Amax,第1个迭代步复用第0步的Amax进行缩放,然后更新计算Amax。第2个迭代步复用第1步更新后的Amax并且再次执行更新,后续迭代以此类推,从而形成“复用—更新”交替进行的统计机制。
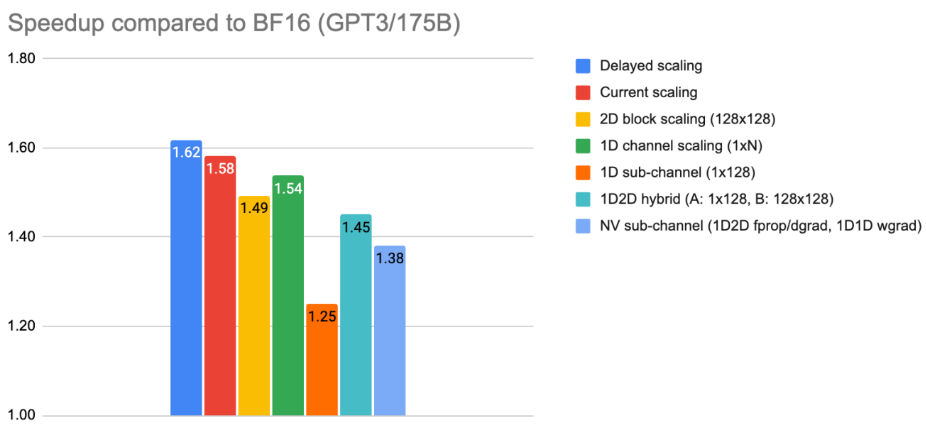
图六. 各种量化粒度的训练性能对比[2]
另一方面,对于单数据格式而言,量化粒度的进一步细化会削弱端到端训练的加速效果。如图六的公开资料显示,无论采用Per-tensor Delayed Scaling还是Per-tensor Current Scaling,其加速比均高于Per-block和Per-channel(即按行或者按列)。并且随着量化粒度不断减小,例如由Per-channel细化至最小的1D Sub-channel(1×128),整体训练加速比呈持续下降趋势。
综合理论分析与公开数据,可以得出如下结论:在保证训练数值稳定性的前提下,采用粗粒度缩放的单数据浮点格式在端到端训练性能上整体优于块浮点格式。同时,随着量化粒度的不断细化,训练加速比呈现单调递减趋势。另一方面,Delayed Scaling的训练性能优于Current Scaling,并且Amax的统计频率越低,其带来的端到端训练加速收益越大。
HiF8对比传统FP8、MXFP8的优势
在Current Scaling策略下,由于Amax由实时数据直接计算,能够准确反映当前激活值的最大幅度,因此不会出现量化上溢的情况。在该设定中,FP8与HiF8在粗粒度下均可实现稳定且等效的训练性能。相比之下,MXFP8在训练过程中的关键路径上引入了更多的量化与反量化操作,因而带来额外开销,从而使其在训练速度上低于FP8与HiF8粗粒度Scaling训练。图五所示的相对BF16的加速比亦验证了该结论:无论是Per-tensor Current Scaling还是Per-tensor Delayed Scaling,其加速性能均显著优于MXFP8。
在Delayed Scaling策略中,Amax由历史统计值预测而来,可能与实际峰值存在偏差,从而引发低比特量化中的上溢风险。因此,该策略对低精度格式的动态范围提出更高要求。传统FP8(E4M3/E5M2)指数范围有限(18或32个阶码),E4M3保证了众数的精度,但是由于动态范围有限,无法很好表达极大值或极小值;E5M2动态范围相对较大,但整体数据精度低于4位有效位的E4M3。无论E4M3还是E5M2,使用粗粒度Delayed Scaling策略,都会降低训练稳定性或者模型的最终质量。HiF8具有锥形精度特征,在提供更大的指数范围(38个阶码)的同时仍保持对众数数据的较高精度。基于此,HiF8能显著降低溢出风险,增强Delayed Scaling训练的稳定性,并在确保端到端精度的同时有效提升整体系统效率。
HiF8更加适用于Delayed Scaling的另一个原因是其可支持更大的量化安全裕度。由于传统FP8-E4M3由于只有18个阶码,因此Nguard往往只能选择0~3这样较小的安全裕度,在X的数值峰值波动较大的时候发生上溢概率高,容易导致训练跑飞。同时也因为安全裕度小,对历史数据的预测不够稳健,只能在每个迭代步计算一次Amax来确保Amax的准确性,导致Amax计算开销大,时延难以掩盖。相对而言,HiF8拥有38个阶码这更大的动态范围,能够Nguard允许选择较大的安全裕度,为不准确的历史Amax近似当前Amax提供了更大的可波动范围,从而大幅提高训练稳健性。此外,较大的安全裕度允许以更低的频率统计更新Amax(如每 5–20 个迭代步更新一次),并可将Amax的计算以通信掩盖方式分摊到多个迭代过程中(将一个Tensor拆分为若干等量子Tensor,分散到Interval次迭代中掩盖),在理想情况下可完全掩盖Amax的计算时延,做完Amax计算完全不影响训练性能。因此在Delayed Scaling框架下,我们可认为HiF8在训练精度和FP8基本一致的前提下,训练性能和稳定性优于FP8。同时,由于MXFP8的训练流程的复杂度提升,HiF8训练性能也会优于MXFP8。
综上所述,HiF8凭借更大的动态范围、更稳健的量化行为以及更低的系统开销,可为业界提供了更适合工业级训练的大规模混合精度方案。
HiF8在小规模模型上的 Per-tensor Scaling预训练实践
5.1 HiF8 Current Scaling训练
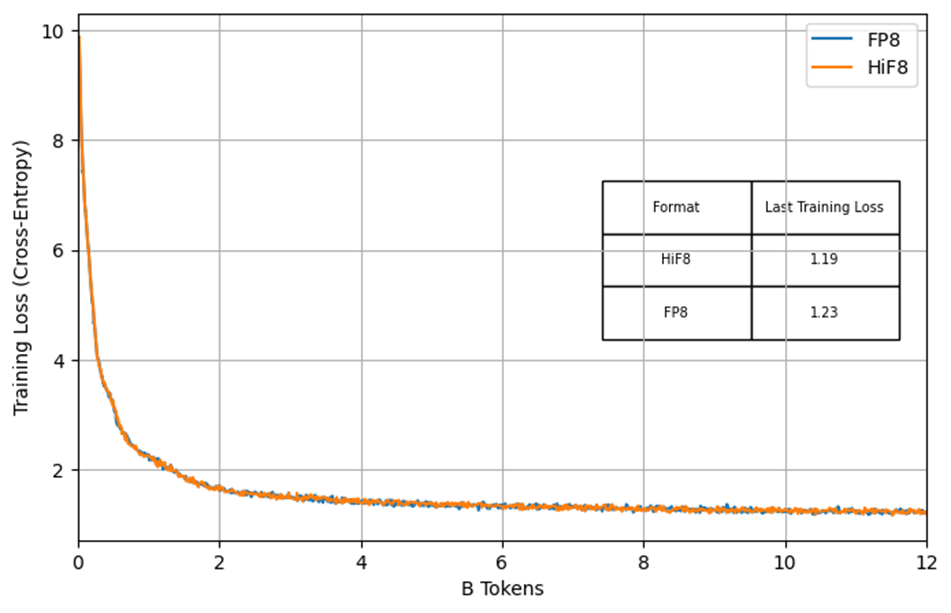
在Current Scaling场景下,我们基于高精度格式仿真HiF8矩阵乘行为的方式,对HiF8在DeepSeek-3B(裁剪版)上的从零开始预训练进行了系统评估。实验采用12B tokens的预训练语料,并使用Per-tensor Current Scaling策略;基线为前向与反向均采用FP8-E4M3的FP8训练流程。实验结果表明,HiF8的训练损失曲线与FP8基线高度一致,几乎完全重叠。同时,在梯度范数(Gradient Norm)方面,HiF8显示出显著更平滑的迭代轨迹,而FP8则呈现明显的毛刺现象,表明HiF8提供的更大动态范围有效提升了训练收敛的稳定性(见图七)。

5.2 HiF8 delayed Scaling训练:学习FP16训练的稳定性技术
在Delayed Scaling场景中,我们同样通过仿真方式评估HiF8的训练效果,采用Per-tensor Delayed Scaling策略对OLMo-1B进行了从零开始的完整预训练。实验采用240B tokens的预训练语料,其中Amax的更新频率设为每5个迭代步更新一次,即Interval = 5。其他迭代步复用最近一次更新的Amax。BF16完整精度的训练作为对照基线。同时,我们提出了一种Delayed Scaling的自动异常检测与校正机制。具体而言,训练初始阶段采用Delayed Scaling,当系统检测到训练过程出现异常行为(例如出现梯度NAN)时,立即通过最近的Checkpoint,重新启动Delayed Scaling训练模式(注意:首次启动Delayed Scaling迭代,没有历史Amax,需要用一次Current Scaling,下一次迭代立即切换到Delayed Scaling)。该机制有效提升了整体训练稳定性并减少异常传播。结果如图八所示,在60000步的迭代中,只在35000步的时候检测到了异常,远低于FP16反向全局Loss Scaling训练策略的异常概率,这进一步说明了HiF8 Delayed Scaling训练稳定性非常高!同时HiF8的训练损失相较BF16的偏差始终低于0.5%,整体Loss曲线与BF16基线高度一致。在下游任务评测中,HiF8相比BF16的准确率损失均小于1%,均值相对BF16提升了0.28个点,达到了精度无损(Lossless)标准。实验结果充分验证了HiF8在Delayed Scaling框架下的稳定性与高效性。
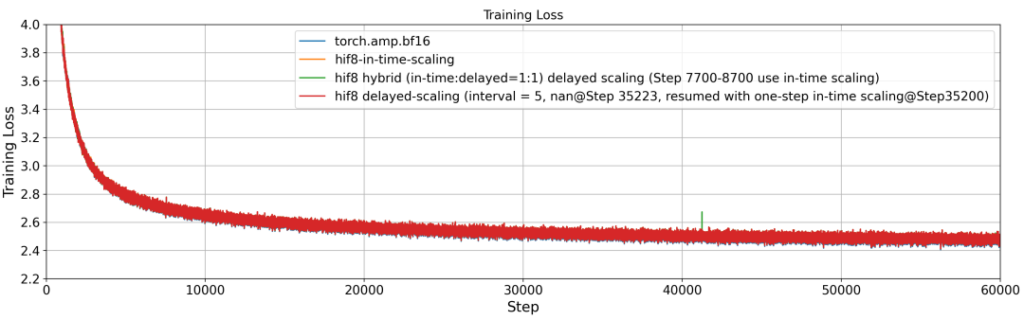
图八. 基于HiF8混合精度的OLMo-1B预训练
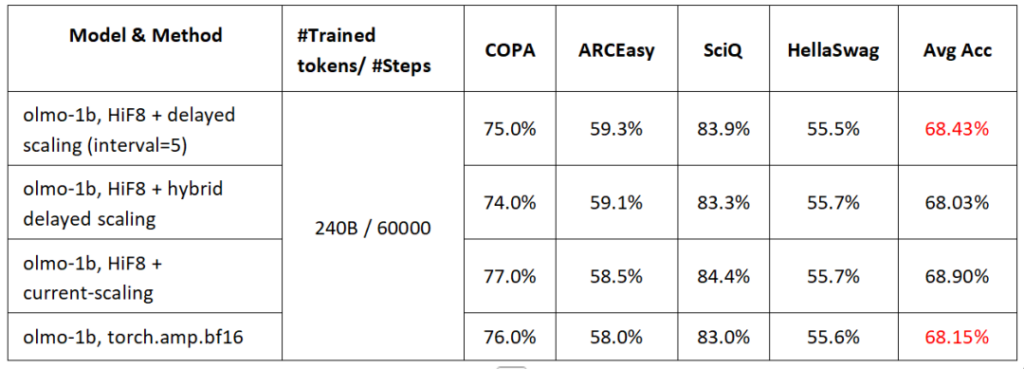
表一. 基于HiF8混合精度预训练的OLMo-1B下游评测任务
综上,我们分别验证了HiF8在Per-tensor Current Scaling与Per-tensor Delayed Scaling两种设置下,在小规模模型完整预训练中的有效性和稳定性。未来,我们将进一步探索HiF8搭配Per-tensor Delayed Scaling在更大规模大语言模型训练中的性能表现,相关结果将于后续工作中报告。
总结
HiFloat8(HiF8)通过创新的浮点数格式设计,呈现出锥形精度特征,显著扩展了可表示的动态范围,从而在混合精度训练中同时兼具高效计算与稳定收敛的优势。在Per-tensor/Per-block Scaling以及Current/Delayed Scaling等关键量化组件中,HiF8均展现出更高的鲁棒性与更低的系统开销。实验结果表明,HiF8在大规模模型预训练中能够保持与高精度 BF16相当的收敛性能,并在多项下游评测任务中实现无损或近乎无损的精度表现。在维持与BF16持平的训练质量的同时,HiF8显著提可提升端到端训练效率,展现出了作为下一代大模型训练核心技术路径的潜在价值。
参考文献
[1]. Rouhani, Bita Darvish, et al. “Microscaling data formats for deep learning.” arXiv preprint arXiv:2310.10537 (2023).
[2]. Stable and Scalable FP8 Deep Learning Training on Blackwell.https://www.nvidia.com/en-us/on-demand/session/gtc25-s72778/
来源:华为技术有限公司供稿
敬请锁定GCC IP栏目CompuWave!GCC智算产业发展委员会持续带来「HiF8」系列专题分享,将邀请技术专家与联创伙伴发掘并向大家呈现HiF8在训练和推理中的优势。
更多HiF8联创合作、进展等信息可联系GCC智算产发委执行秘书长熊华(xionghua@gccorg.com)获取。
