《老子到此一游系列》之 老子带你看懂这些风景—— 多维探秘通用无损压缩 第一章 熵编码器/第二章 BWT 算法（转发）

《老子到此一游系列》之 老子带你看懂这些风景—— 多维探秘通用无损压缩 第一章 熵编码器/第二章 BWT 算法（转发）

ELT.ZIP是谁？

ELT<=>Elite(精英)，.ZIP为压缩格式，ELT.ZIP即压缩精英。

成员：

上海工程技术大学大二在校生 闫旭

合肥师范学院大二在校生 楚一凡

清华大学大二在校生 赵宏博

成都信息工程大学大一在校生 高云帆

黑龙江大学大一在校生 高鸿萱

山东大学大三在校生 张智腾

ELT.ZIP是来自6个地方的同学，在OpenHarmony成长计划啃论文俱乐部里，与来自华为、软通动力、润和软件、拓维信息、深开鸿等公司的高手一起，学习、研究、切磋操作系统技术…

本文的梳理来自其中的四名同学：闫旭、楚一凡、赵宏博和高云帆。

引言

压缩的标准方法是定义产生不同类型数据源的类别，假设数据是由某一类源产生的，并应用为其特殊设计的压缩算法，若可以在近似为输出的数据上良好运行，便可被称为通用压缩算法。

第一章  熵编码器

熵编码器（Entropy Coder）是一种根据字符出现的概率为字母表中的每个字符分配编码的方法。更有可能出现的字符被分配的编码比不太可能出现的更短，这种方式可以使压缩序列的预期长度最小。目前流行的熵编码器是Huffman编码器和算术编码器，这两种方法都做到了相对最优，所以不能分配比预期长度更小的压缩序列编码。其中，Huffman在分配整数长度编码的方法类中是最优的，算术编码则不受这种限制，因此，它通常可产生更短的期望编码长度。

图1：序列abracadabra的Huffman树 

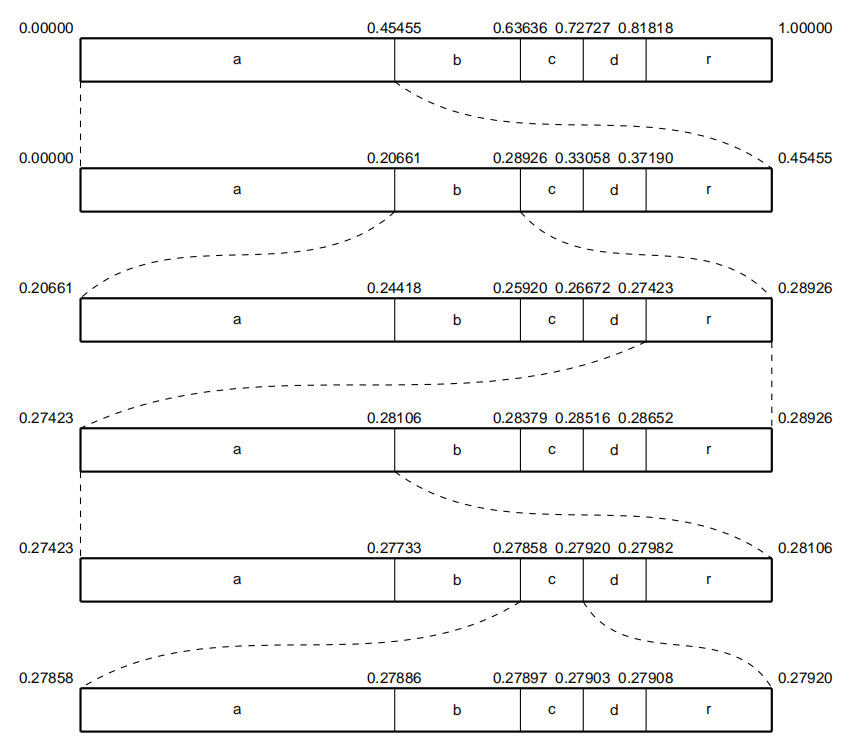
图2：算术编码过程

第二章  BWT算法

块排序压缩算法（Block-sorting Compression Algorithm），通常被称为Burrows-Wheeler变换算法（Burrows–Wheeler Compression Algorithm），是一个被应用在数据压缩技术（如bzip2）中的算法，于1994年被Michael Burrows和David Wheeler在位于加利福尼亚州帕洛阿尔托的DEC系统研究中心发明。

图3：（a）David Wheeler （b）Michael Burrows

2.1 基本原理

  1. 构造矩阵，其行存储压缩序列的所有单字符循环移位
  2. 按字典顺序对行进行排序
  3. 使用矩阵最后一列进行后续处理

BWT算法与以往的压缩算法有所不同，比较著名的压缩算法如Lempel-Ziv(LZ77，LZ78)、PPM、DMC针对的是通用的数据流模型，比如无记忆源(Memoryless Sources)，马尔可夫源(Markov sources),有限阶FSM源(Finite-order FSM Sources),一次读取一个或多个字节，而BWT可以处理成块的数据。BWT算法的核心思想是对一个字符串中的字符进行位置变换，使相同的字符相邻的概率增大。

上述过程被称为Burrows-Wheeler变换*（BWT）。随后，变换的输出由一个前移变换处理，最后阶段，由熵编码器压缩，可以是Huffman编码或算术编码。结果是，获得了一个序列，其中出现在相似上下文中的所有字符被分组。

字符串经过BWT算法转换后并没有被压缩，而是因其极有规律性的字母内聚的特点使其他文本压缩算法大大简化，提高压缩速率和压缩比。基于BWT算法的重要特点是运行速度快、压缩比合理，比LZ算法好得多，只比现有最佳部分匹配（PPM, prediction by partial matching）算法稍差；是Ziv-Lempel快速压缩算法和PPM算法的有趣替代品，前者压缩比较差，后者压缩比较好，但工作速度较慢。

2.2 算法详述

对于一个长度为n的序列x，可以将序列轮转形成一个的矩阵：

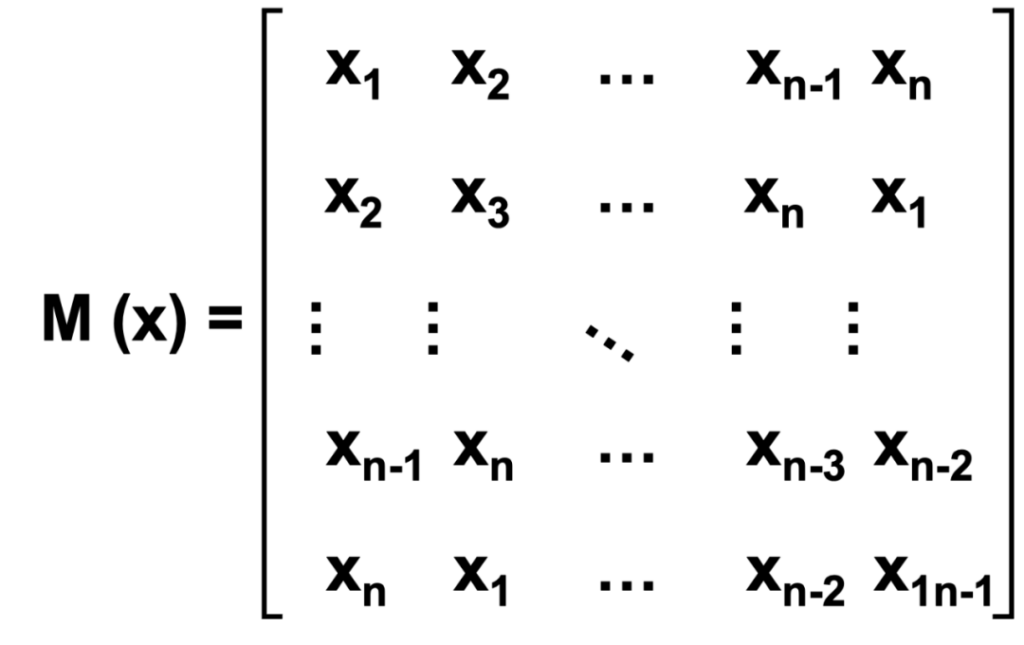
然后将矩阵以行为单位按照字母表顺序重新排列成矩阵，得到，并用R(x)记录在新矩阵中原序列x所在的行数。取矩阵的最后一列记为即得到BWT的最终结果。

下面我们用字符序列x=“abracadabra”，且为了获得更好的关系类型的序列，我们在x前加上哨兵字符“$”。最终得到xbwt= $drcraaaabba，R(x) = 1。可以看出通过BWT算法，一些字符连续出现的概率增大。

BWT算法的逆过程则比较复杂，但在编程实现上也比较简单。其主要思想是以xbwt为基础，对字符序列进行转移、排序和组合构建BWT转换后得到的矩阵M~(x)。还是以$drcraaaabba为例：

按照这样的规律一直操作下去，最终可以得到：

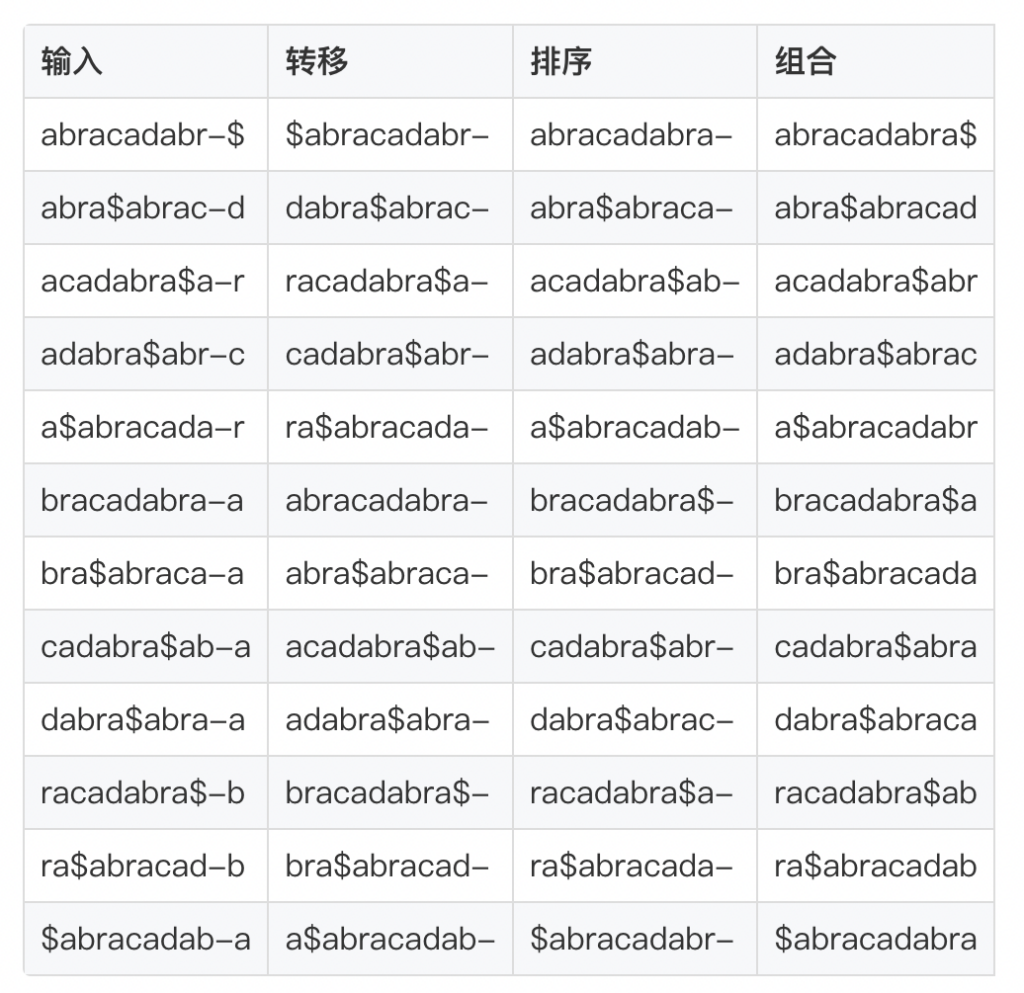
最后一次操作的得到的组合即为x对应的矩阵M~(x)，矩阵的第一行去掉最后的“$“就得到原字符序列x=”abracadabra”。

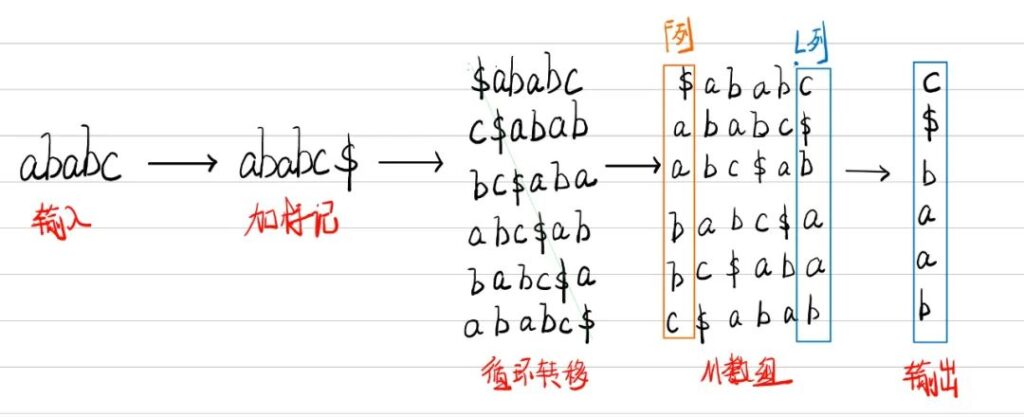
BWT就是一个加标记，循环转移，算出数组，输出结果的过程。

① 这里我们输入字符串ababc，并给其加上标记得到ababc$这个标记$要比所有字符都要小。

② 之后我们对处理后的字符串进行循环转移，此时你可以把ababc$当作一个圆，然后让其旋转，使得F列（第一列）的字符按照ASCII码从小到大排列。

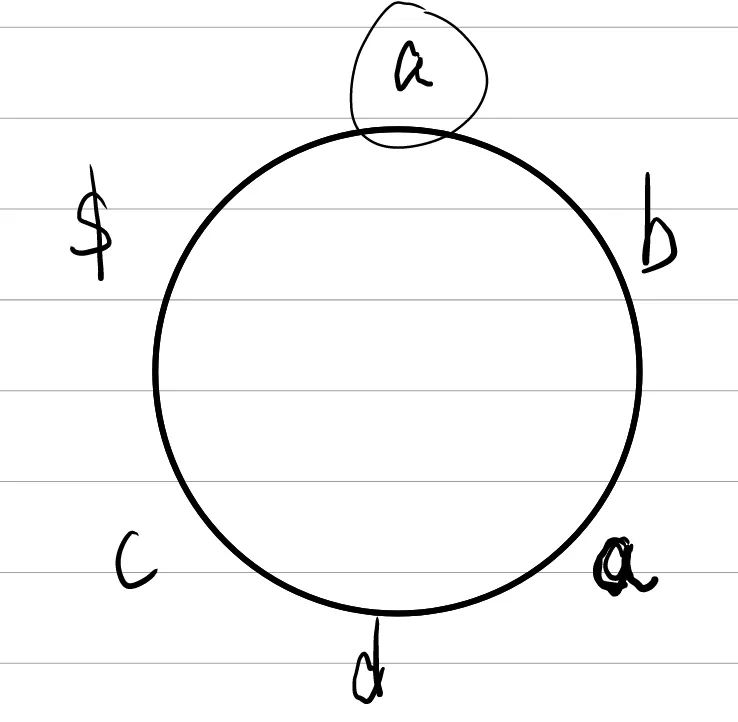
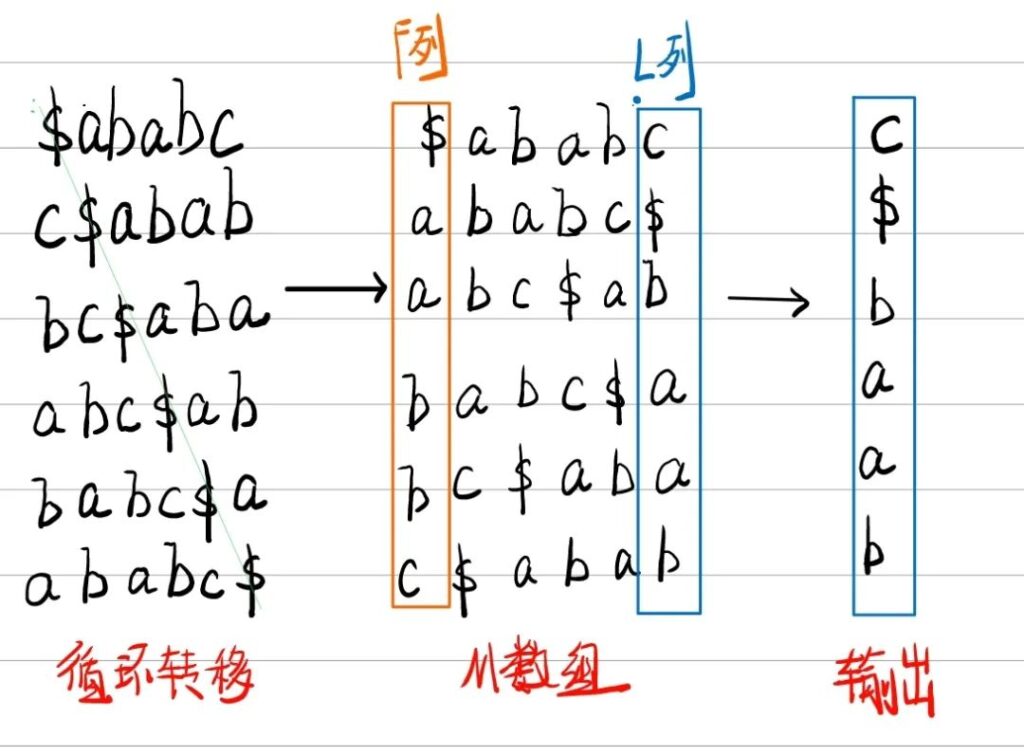
③ 得到的M数组最后一列便是输出的L列。

2.3 BWT编码及解码的C++实现

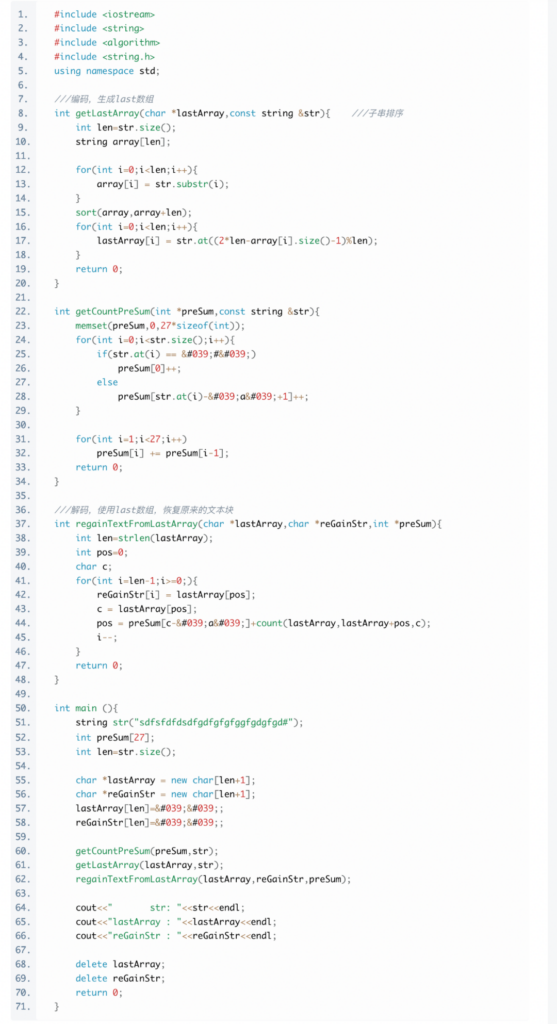
研究者提出一种基于 Burrows-Wheeler 变换的改进算法，该算法在获得最佳压缩比的同时，其运算速度可以与该类算法中最快的算法媲美。我们下文再讲。

参考文献

[1] Deorowicz S . Universal Lossless Data Compression Algorithms[J]. Philosophy Dissertation Thesis, 2003.

https://www.researchgate.net/publication/2910531_Universal_Lossless_Data_Compression_Algorithms

[2] Burrows M , Wheeler D J . A Block-Sorting Lossless Data Compression Algorithm[J]. technical report digital src research report, 1995.

https://www.researchgate.net/publication/2702058_A_Block-Sorting_Lossless_Data_Compression_Algorithm

[3] Gao X , Dong M , Miao X , et al. EROFS: a compression-friendly readonly file system for resource-scarce devices. 2019.

https://dl.acm.org/doi/abs/10.5555/3358807.3358821

[4] Ni G . Research on BWT and Classical Compression Algorithms[J]. Computer & Digital Engineering, 2010.

http://en.cnki.com.cn/Article_en/CJFDTOTAL-JSSG201011009.htm

[5] Farruggia A , Ferragina P , Frangioni A , et al. Bicriteria data compression[J]. Society for Industrial and Applied Mathematics, 2013.

https://xueshu.baidu.com/usercenter/paper/show?paperid=27a6024fe31d2cda63a5e79b34be6cfd

[6] Alakuijala J , Farruggia A , Ferragina P , et al. Brotli: A General-Purpose Data Compressor[J]. ACM Transactions on Information Systems, 2018, 37(1):1-30.

https://xueshu.baidu.com/usercenter/paper/show?paperid=1w6v0jh0qj360210sn0p08f0br369452&site=xueshu_se&hitarticle=1

[7] Overview – The Hitchhiker’s Guide to Compression (go-compression.github.io)

https://go-compression.github.io/

[8] Wavelet Tutorial – Part 1

https://users.rowan.edu/~polikar/WTpart1.html

[9] Wavlet Tutorial – Part 2

https://users.rowan.edu/~polikar/WTpart2.html

[10] Wavelet Tutorial – Part 3

https://users.rowan.edu/~polikar/WTpart3.html

缩略语列表

缩写英文中文
ANSAsymmetric numeral systems非对称数字系统
BSLDCAThe Block Sorting Lossless Data Compression Algorithm块排序无损数据压缩算法
BTWBurrows–Wheeler  TransformBurrows–Wheeler转换
BWCABurrows-Wheeler Compression AlgorithmBurrows-Wheeler压缩算法
CTWContext Tree Weighting上下文树加权
CWTContinue Wavelet Transform连续小波变换
DMCDynamic Markov Coding动态马可夫压缩
DWTDiscrete Wavelet Transform离散小波变换
ECEntropy Coder熵编码器
MCOMulti-Criteria Optimisation多标准优化
MTFMove To Front Transform前移变换
PPMPrediction by Partial Matching通过部分匹配进行预测
RLE-0Zero Run Length Encoding零游程编码
STFTShort-time Fourier transform短时傅里叶变换

写在最后：

OpenHarmony 成长计划—“啃论文俱乐部”（以下简称“啃论文俱乐部”）是在 2022年 1 月 11 日的一次日常活动中诞生的。截至 3 月 31 日，啃论文俱乐部已有 87 名师生和企业导师参与，目前共有十二个技术方向并行探索，每个方向都有专业的技术老师带领同学们通过啃综述论文制定技术地图，按“降龙十八掌”的学习方法编排技术开发内容，并通过专业推广培养高校开发者成为软件技术学术级人才。

啃论文俱乐部的宗旨是希望同学们在开源活动中得到软件技术能力提升、得到技术写作能力提升、得到讲解技术能力提升。大学一年级新生〇门槛参与，已有俱乐部来自多所高校的大一同学写出高居榜首的技术文章。

如今，搜索“啃论文”，人们不禁想到、而且看到的都是我们——OpenHarmony 成长计划—“啃论文俱乐部”的产出。

OpenHarmony开源与开发者成长计划—“啃论文俱乐部”学习资料合集

1）入门资料：啃论文可以有怎样的体验  

https://docs.qq.com/slide/DY0RXWElBTVlHaXhi?u=4e311e072cbf4f93968e09c44294987d

2）操作办法：怎么从啃论文到开源提交以及深度技术文章输出https://docs.qq.com/slide/DY05kbGtsYVFmcUhU  

3）企业/学校/老师/学生为什么要参与 & 啃论文俱乐部的运营办法https://docs.qq.com/slide/DY2JkS2ZEb2FWckhq

 4）往期啃论文俱乐部同学分享会精彩回顾： 

同学分享会No1.成长计划啃论文分享会纪要（2022/02/18）  https://docs.qq.com/doc/DY2RZZmVNU2hTQlFY  

同学分享会No.2 成长计划啃论文分享会纪要（2022/03/11）  https://docs.qq.com/doc/DUkJ5c2NRd2FRZkhF  

同学们分享会No.3 成长计划啃论文分享会纪要（2022/03/25） 

https://docs.qq.com/doc/DUm5pUEF3ck1VcG92?u=4e311e072cbf4f93968e09c44294987d

现在，你是不是也热血沸腾，摩拳擦掌地准备加入这个俱乐部呢？当然欢迎啦！啃论文俱乐部向任何对开源技术感兴趣的大学生开发者敞开大门。

后续，我们会在服务中心公众号陆续分享一些 OpenHarmony 开源与开发者成长计划—“啃论文俱乐部”学习心得体会和总结资料。记得呼朋引伴来看哦。

扫码添加 OpenHarmony 高校小助手，加入“啃论文俱乐部”微信群