细数生活中的压缩点滴 第三章 基于稀疏快速傅里叶变换(SFFT)的语音压缩算法

文章转发自51CTO【ELT.ZIP】OpenHarmony啃论文俱乐部——细数生活中的压缩点滴
项目介绍
3.1 SFFT的前世今生
1876 年 Bell 发明创造了电话,用声电-电声转换方式实现了人类有史以来第一次的远距离语音传输,开启了现代语音信号处理的研究。
1928年奈奎斯特(Nyquist)就推导出在理想低通信道的最高码元传输速率的公式。
2012 年由麻省理工学院(Massachusetts Institute of Technology,MIT)Haitham Hassanieh 等四位研究员提出的一种新的信号处理算法,稀疏快速傅里叶变换(Sparse Fast Fourier Transform,SFFT) 。该算法通过利用信号频域的稀疏特性,以与信号长度成亚线性关系的时间复杂度和较高的概率重构出信号的完整频谱,其效率是传统快速傅里叶变换(Fast Fourier Transform,FFT)算法的 10~100 倍。为此,麻省理工学院专门建立了研究 SFFT 的相关网站,并发表了多篇相关论文。
3.2 应用场景
语言交流是人类最基本的能力之一,是人类长期进化形成的特有的思维和交流形式。语言是概况总结的规律性的符号系统,是创造和记录人类文明的根本方式。
语音作为语言的声学表现形式,是音与义的结合体,是最方便有效的信息传递和交换形式。语音和语言是人类思维的一种依托,它与所生存的社会、文化密切相关,拥有最大的信息含量及最高的智慧水平。
语音信号的数字化处理已成为数字化时代下通信网络里最重要的一部分,数字语音信号的传输、合成、存储、增强、识别等已经有了比较成熟的技术,语音压缩算法在此基础之上拥有了蓬勃发展的机会。
语音信号处理技术的应用包括工业、军事、交通、医学、民用等多种领域,市场上已有大量的语音相关产品,语音信号方向的科研及应用拥有极为广阔的市场需求及应用场景。
3.3 语音信号压缩面临的问题
传统的信号离散化基本依据为奈奎斯特(Nyquist)采样定理,指出当采样频率 f 大于信号最高频率的 2 倍时,采样后的数字信号完整地保留了原信号中的信息,而在实际应用中往往需要 5~10 倍才能达到理想的效果。这给信息处理带来了巨大压力:
- 需要提高采样频率来完成超宽带信号的信息采集,硬件要求高、设备昂贵、难于实现;
- 采样信息庞大,需要的更多的存储介质。\

在随着移动互联网等的快速发展,语音业务也大幅增加,用传统奈奎斯特采样将会获得庞大的采样数据,这给信号的传输和存储带来了巨大压力。而此时,如何有效降低传输和存储所需的数据量成为了缓解硬件设备的压力,降低时延,是提高信息传输的整体效率的关键问题。
3.4 关键技术
MIT提出的稀疏快速傅里叶变换(SFFT)技术将语音信号内的冗余部分找到,并且在保持可接受失真的情况下尽可能多的将冗余部分删除,使用较少的比特数表示原始信号。最后,利用这些较少的比特数,通过反变换算法将语音信号以高概率重构出来。
简而言之,利用信号频域具有稀疏性的特点,抽取有用特征点,去除无用信号, 减少信号变换过程中的运算时间和存储单元,达到压缩数据的效果。
3.5 理论框架
SFFT 算法大致可以分为三个步骤:
3.5.1 “分筐”
首先将长度为 N 的信号频率系数按规律 H 投入 B 个“筐”中,即分筐:
很明显,在分筐的过程中数据量下降了。
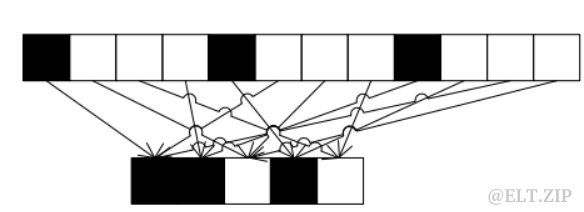
3.5.2 FFT降采样
对分筐后的信号进行降采样 FFT。
3.5.3 重构信号
最后依据分筐时的各种参数设计出重构算法,以高概率重构出大频率系数的位置和幅值,得到重构信号的频谱。
根据上面的分析可以得到如下 SFFT 的理论框架框图:
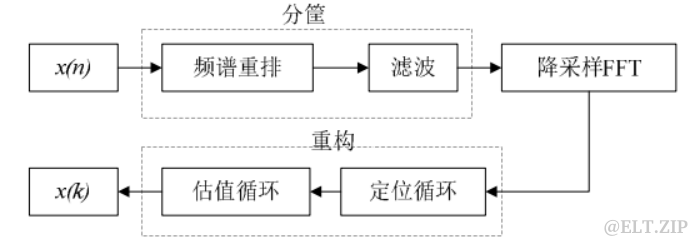
3.5.4 总结:
- 所谓分筐即抽取有用特征点,去除无用信号。
- 降采样,即是采样点数减少的FFT。
- 重构,即重构出大频率系数的位置和幅值,得到重构信号的频谱,即还原出音频信号。
- 我们发现分筐与降采样的过程抽取出了有用信号,去除了无用信号,从而大幅度压缩了数据量,从而实现了缓解硬件设备的压力,降低时延,提高信息传输的整体效率的目的。
3.6 算法评估
3.6.1 分筐效果
频域效果分析:

时域效果分析:
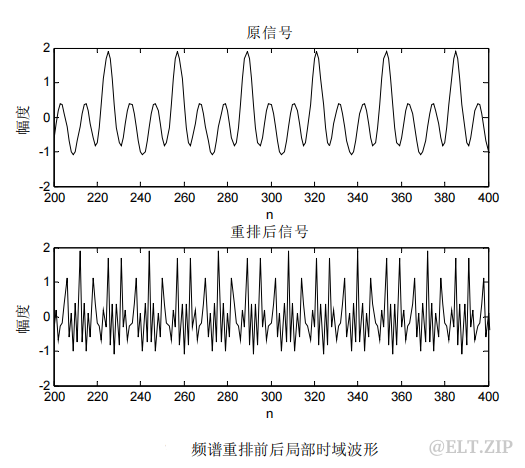
可以看出频域与时域信号明显密集化。
3.6.2 重构信号与原信号对比
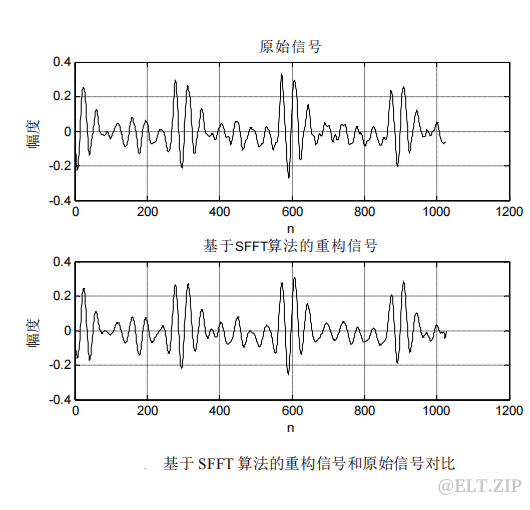
可以看出信号高度相似,差异很小。
综上,采用高效的 SFFT 算法对其语音信号进行压缩处理,在接收端通过高概率重构得到原始信号的近似信号。在语音信号传输前通过有效的压缩方法剪去信号内部的冗余部分,利用较少的数据量便可以完成信号的高效传输。
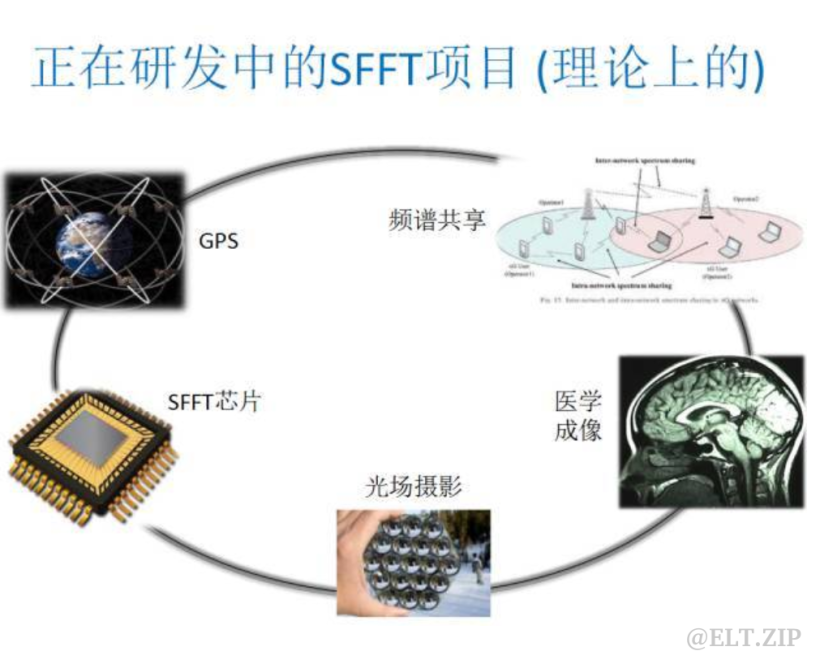
3.7 其他应用场景
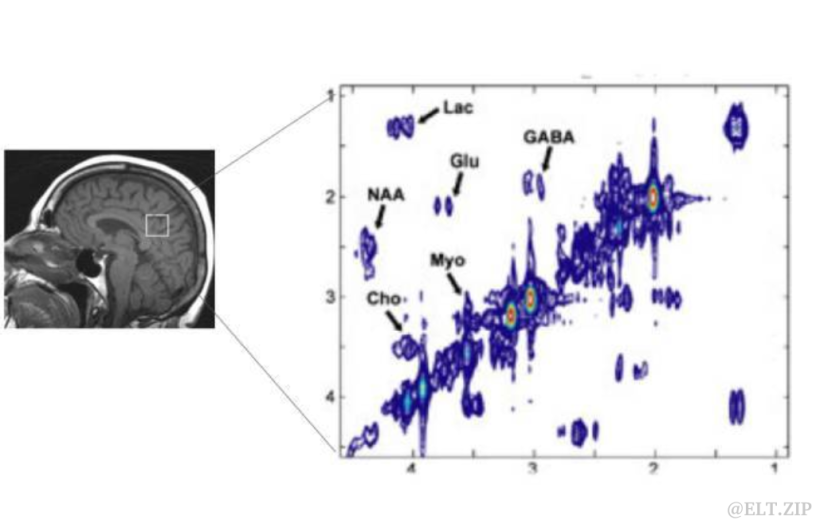
医学成像大多数的医学图像具有稀疏特性,将 SFFT 运用在 2D 相关振动光谱技术成像中, 降低了扫描时间、减少了截断伪影。
频谱感知由于对 GHz 带宽的信号检测会带来超高的采样频率并获得海量采样数据,给硬件设备提出了巨大的挑战。采用混叠同余类似方法,无需全带采样实现信号的频谱计算,高效减少检测时间和降低能耗。

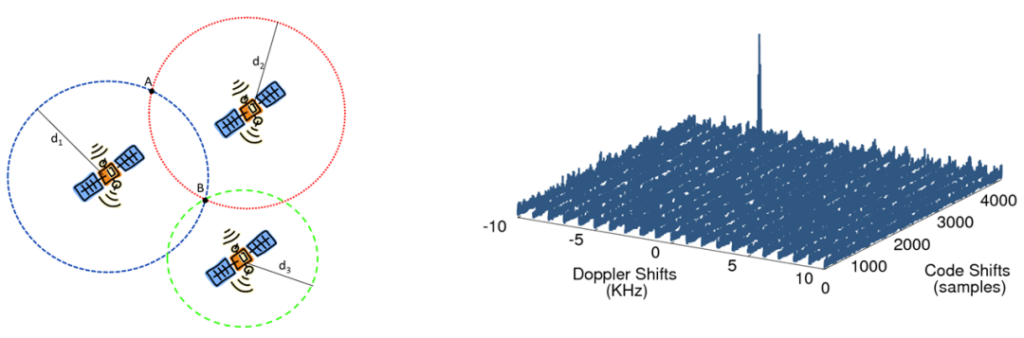
GPS 导航在卫星传输过程中通常使用伪随机前导码来实现同步,存在较大的时延。基于前导码良好的自相关性,使用 SFFT 技术加快了 GPS 的同步处理能力。
语音信号处理,埃及-日本科学技术大学的研究人员在语音信号处理中采用了基于 SFFT 算法的处理方法。
在国内,SFFT 算法还处在研究的起步阶段,在水声快速解调算法、宽带频谱感知、直接序列扩频信号的捕获、计算外辐射源雷达互模糊函数等做了一定的研究。综上不难发现,该算法拥有广阔的应用前景。
技术DNA
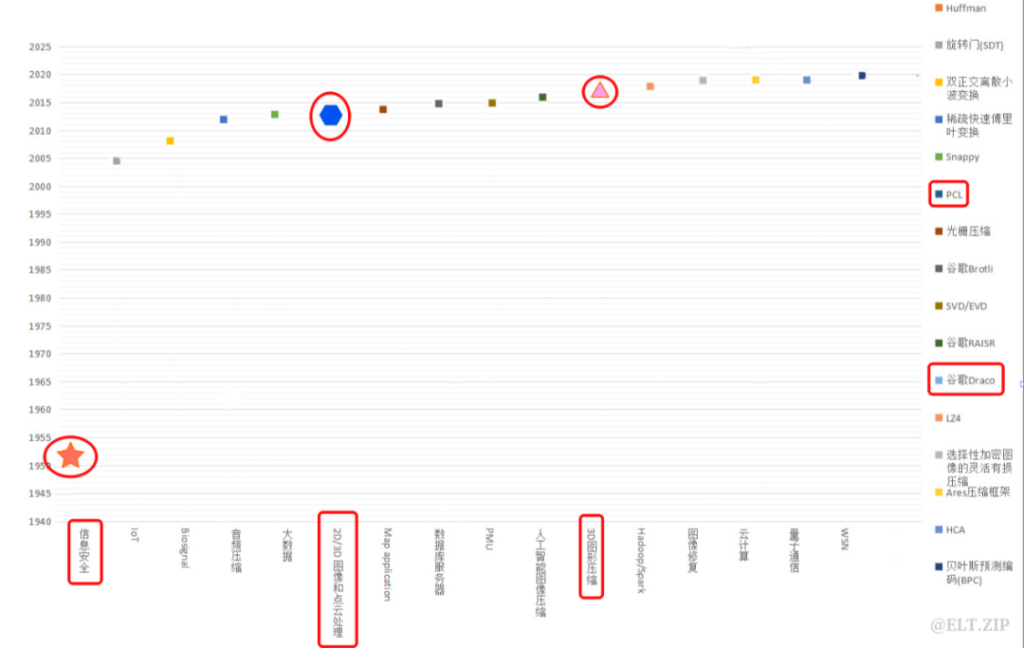
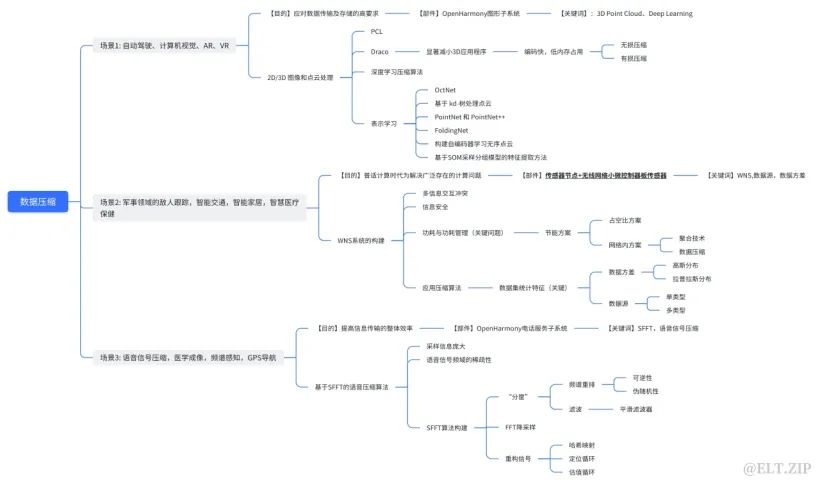
智慧场景
后期预告
第三章 基于稀疏快速傅里叶变换(SFFT)的语音压缩算法
参考文献
[1] Huang T, Liu Y. 3d point cloud geometry compression on deep learning[C]//Proceedings of the 27th ACM international conference on multimedia. 2019: 890-898.
https://dl.acm.org/doi/abs/10.1145/3343031.3351061
[2] Rusu R B, Cousins S. 3d is here: Point cloud library (pcl)[C]//2011 IEEE international conference on robotics and automation. IEEE, 2011: 1-4.
https://ieeexplore.ieee.org/abstract/document/5980567/
[3] Guo Y, Wang H, Hu Q, et al. Deep learning for 3d point clouds: A survey[J]. IEEE transactions on pattern analysis and machine intelligence, 2020, 43(12): 4338-4364.
https://ieeexplore.ieee.org/abstract/document/9127813/
[4] Chen D Y, Tian X P, Shen Y T, et al. On visual similarity based 3D model retrieval[C]//Computer graphics forum. Oxford, UK: Blackwell Publishing, Inc, 2003, 22(3): 223-232.
https://onlinelibrary.wiley.com/doi/abs/10.1111/1467-8659.00669
[5] Srisooksai T, Keamarungsi K, Lamsrichan P, et al. Practical data compression in wireless sensor networks: A survey[J]. Journal of network and computer applications, 2012, 35(1): 37-59.
https://www.sciencedirect.com/science/article/abs/pii/S1084804511000555
[6] 刘清华. 基于稀疏快速傅里叶变换的语音压缩处理算法研究[D]. 兰州交通大学, 2016.
https://cdmd.cnki.com.cn/Article/CDMD-10732-1016275325.htm
[7] Smith C A. A survey of various data compression techniques[J]. Int J pf Recent Technol Eng, 2010, 2(1): 1-20.
[8] 人工智能之表示学习
https://static.aminer.cn/misc/pdf/RepLearning.pdf
[9] 干货 | 用深度学习设计图像视频压缩算法:更简洁、更强大
https://cloud.tencent.com/developer/article/1061252
[10] 大数据可变革医疗保健行业
https://cn.micron.com/insight/big-data-can-revolutionize-health-care
ELT.ZIP是谁?
ELT<=>Elite(精英),.ZIP为压缩格式,ELT.ZIP即压缩精英。
成员:
上海工程技术大学大二在校生 闫旭
合肥师范学院大二在校生 楚一凡
清华大学大二在校生 赵宏博
成都信息工程大学大一在校生 高云帆
黑龙江大学大一在校生 高鸿萱
山东大学大三在校生 张智腾

ELT.ZIP是来自6个地方的同学,在OpenHarmony成长计划啃论文俱乐部里,与来自华为、软通动力、润和软件、拓维信息、深开鸿等公司的高手一起,学习、研究、切磋操作系统技术…
写在最后:
OpenHarmony 成长计划—“啃论文俱乐部”(以下简称“啃论文俱乐部”)是在 2022年 1 月 11 日的一次日常活动中诞生的。截至 3 月 31 日,啃论文俱乐部已有 87 名师生和企业导师参与,目前共有十二个技术方向并行探索,每个方向都有专业的技术老师带领同学们通过啃综述论文制定技术地图,按“降龙十八掌”的学习方法编排技术开发内容,并通过专业推广培养高校开发者成为软件技术学术级人才。
啃论文俱乐部的宗旨是希望同学们在开源活动中得到软件技术能力提升、得到技术写作能力提升、得到讲解技术能力提升。大学一年级新生〇门槛参与,已有俱乐部来自多所高校的大一同学写出高居榜首的技术文章。
如今,搜索“啃论文”,人们不禁想到、而且看到的都是我们——OpenHarmony 成长计划—“啃论文俱乐部”的产出。
OpenHarmony开源与开发者成长计划—“啃论文俱乐部”学习资料合集
1)入门资料:啃论文可以有怎样的体验
https://docs.qq.com/slide/DY0RXWElBTVlHaXhi?u=4e311e072cbf4f93968e09c44294987d
2)操作办法:怎么从啃论文到开源提交以及深度技术文章输出https://docs.qq.com/slide/DY05kbGtsYVFmcUhU
3)企业/学校/老师/学生为什么要参与 & 啃论文俱乐部的运营办法https://docs.qq.com/slide/DY2JkS2ZEb2FWckhq
4)往期啃论文俱乐部同学分享会精彩回顾:
同学分享会No1.成长计划啃论文分享会纪要(2022/02/18) https://docs.qq.com/doc/DY2RZZmVNU2hTQlFY
同学分享会No.2 成长计划啃论文分享会纪要(2022/03/11) https://docs.qq.com/doc/DUkJ5c2NRd2FRZkhF
同学们分享会No.3 成长计划啃论文分享会纪要(2022/03/25)
https://docs.qq.com/doc/DUm5pUEF3ck1VcG92?u=4e311e072cbf4f93968e09c44294987d
现在,你是不是也热血沸腾,摩拳擦掌地准备加入这个俱乐部呢?当然欢迎啦!啃论文俱乐部向任何对开源技术感兴趣的大学生开发者敞开大门。

扫码添加 OpenHarmony 高校小助手,加入“啃论文俱乐部”微信群
后续,我们会在服务中心公众号陆续分享一些 OpenHarmony 开源与开发者成长计划—“啃论文俱乐部”学习心得体会和总结资料。记得呼朋引伴来看哦。
